从几何意义到良好递归——一个欧几里得算法的重新诠释

1729 字约 6 分钟

2026-02-14

本文原文为英文（嗯是我自己写的），使用Qwen-3-Max翻译并人工校对，改正了一些不自然的地方～

引言

在上我们抽代的Tutorial的时候，老师出了一个十分好玩的题——欧几里得算法究竟是怎么回事？

很多时候，很多课程只是直接教了欧几里得算法本身和其证明，草草带过，了事便是。我曾经一度认为它就是纯魔法。我要验算法， $\gcd(n,m) = \gcd(m,n \mod m)$ 呗，又是欧几里得这个天才想出来的小东西，完活，算法没有问题。

而真正的转折点则始于我尝试将它与几何直觉联系起来之时。

是否能被恰好塞满的几何直觉

假设我们正在求 $\gcd(n,m)$ ，其中 $n,m\in \mathbb{Z}$ 。为简化起见，我们始终假设 $n \geq m > 0$ 。

考虑一个面积为 $n$ 的矩形和另一个面积为 $m$ 的矩形。在此方法中，我们完全可以把矩形的具体长或宽扔一边去，没有必要管。我们接下来则试图检验：若干个面积为 $m$ 的矩形能否恰好填满面积为 $n$ 的大矩形。注意，只要不改变面积，我们可以自由调整矩形的长和宽。

如果整数个面积为 $m$ 的矩形恰好能填满面积为 $n$ 的大矩形，那我们就证明了 $m$ 是 $n$ 的一个因数，进而结束。此步骤等价于以下公式：

n = mq + 0, \quad q\in\mathbb{N}

如果不能恰好填满，则会产生一块尚未被填充的“空白区域”。注意，这正对应于余数，记为 $r$ 。我们生成一个面积为 $r$ 的矩形。此步骤等价于以下公式：

n = mq + r, \quad 0 \le r < m

根据欧几里得算法，下一步应该求的是 $\gcd(m,r)$ 。怎么求呢？我们再对这俩数执行相同的操作，即检验多少个面积为 $r$ 的矩形能填入面积为 $m$ 的大矩形。如此递归反复，直到达到大矩形能被整数个小矩形恰好填满的条件。由于这些矩形都是基于余数（矩形）生成的，我们最终找到的最大矩形（将不留任何余数，即空白）将自动适配整个原始矩形。最坏的情况是它被面积为 1 的矩形填满，这必然可行，因为我们处理的是自然数，不涉及小数。

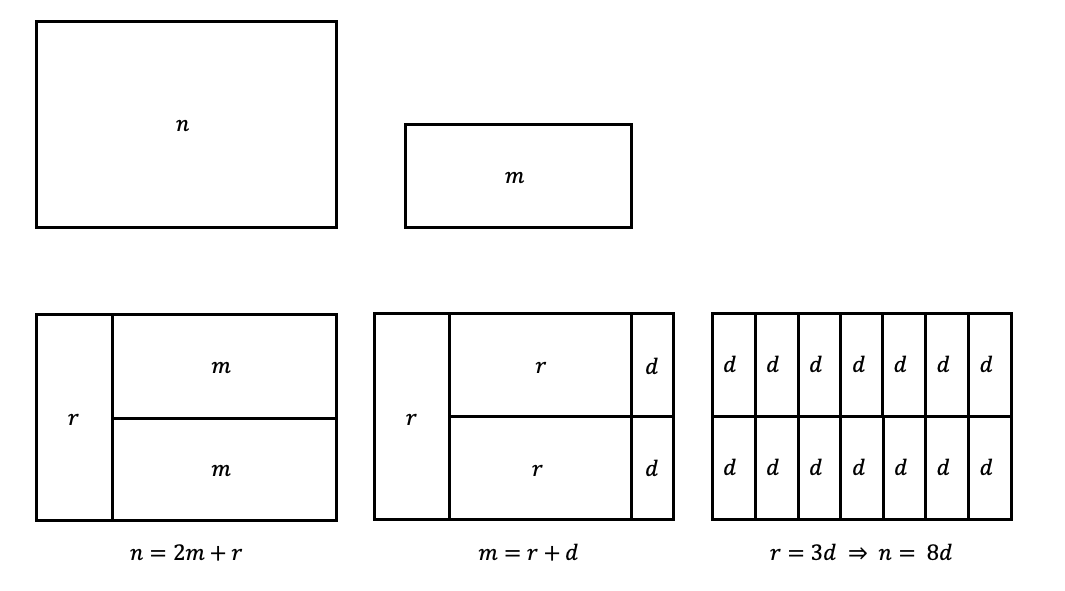
例如，下图（未按比例绘制，仅作示意）展示了这一流程。考虑两个矩形，我们开始检验大矩形能容纳多少个小矩形，然后继续递归执行，最终发现面积为 $d$ 的矩形组合在一起，恰恰好好能填满面积为 $n$ 的大矩形。

代码实现

那都做到这步了，不如直接把代码写出来吧，也能从逻辑上验证我的构想是否正确不是。因此，我用 Haskell 编写了如下代码来实现这一思路：

-- pre-condition: n >= m > 0
divi :: Int -> Int -> (Int,Int)
divi n m =
	go n m 1
		where
		go n m r
			| m*r < n = go n m (r+1)
			| m*r == n = (r,0)
			| otherwise = (r-1, n-m*(r-1))
-- post-condition: 元组，第一个数是银子，第二个数是余数

-- pre-condition: n>m
euc :: (Int, Int) -> Int
euc (n, m)
	| m == 0 = n
	| otherwise = let (_, r) = divi n m
				  in euc (m, r)

第一个函数是 divi。接收两个矩形的面积（一个大矩形和一个小矩形），然后找出大矩形能容纳多少个小矩形，以及剩余的空白区域。通过试错法递归执行此操作（若仍有空间则前进一步，若已超出则回退一步），等价于接收两个数并求出商和余数（即返回 $m=nq+r$ 中的 $(r,q)$ ）。

第二个函数是 euc。调用 divi 函数，尝试基于余数找到能整除大矩形的最大矩形，在结构上等价于欧几里得算法的实现。

我们可以很明显的注意到，该实现与欧几里得算法同构，因此它是正确的。为了防止被揍，我们还是来个系统的正确性证明吧。

正确性证明

终止性。 试证 euc (n,m) 必然终止。根据定义可知，余数严格小于被除数本身。由前提条件知 $n \geq m$ 。因此，在每次递归步骤中，输入对的第二个分量严格递减。由于自然数集是良序的且不存在无穷递降，输入元组的第二个元素终将在某一步达到 0，从而终止。

正确性。 已知对于 $n=km+r$ 且 $0 \leq r < m$ ， $\gcd(m,n)=\gcd(n,r)$ 成立。从代码及其后置条件可知，该构造确实计算出了这样的对 $(k,r)$ 。由于 divi 正是按此方式构造的，每一步递归都保持了最大公约数不变。证毕。

或许我们还可以从这个证明中得到一个点：欧几里得算法本质上是递归的，且基于自然数的良序性。是的，数学和计算机之间的联系很曼妙。

该方法的推广与抽象，及其他

由于该方法不依赖矩形的具体长或宽，这促使我思考一种十分抽象的抽象：这个解释能否推广到其他形状？

我们当然也能将其推广到纯正方形，因为正方形是矩形的特殊情况。我们所用的形状必须支持“切割”与“拼接”操作。我又去找ChatGPT问了问，结果很明确：要完成这一探索，我需要测度论的知识（裂开）。

大家可能也注意到了，这段Haskell代码里 divi 的时间复杂度为 $O(n)$ 。我目前保留了这一粗糙的结构，但我们完全可以在保持语义不变的前提下对其进行优化，比如说试着动态调整每次尝试调整的步长！

最后，恭祝大家新春快乐！对我来说这个蛇年过得挺充实的，挺忙的，也挺抽象的。祝大家马年万事顺心吧，今年春节刚好赶上Reading Week能放假一周，不过这一周还是回不去国啊（悲）。算了各位。

祝大家马年大吉，万事如意，所有证明的“Aha Moment”都如期而至。

濮弘文
英国，伦敦
2026 年 2 月 14 日

有任何问题？欢迎通过微信或邮件联系我！微信 @ boypu123（添加好友时请备注“来自博客”）；邮箱：hongwen.pu@outlook.com 或 hongwen.pu.25@ucl.ac.uk。